

If I have K=1 and reinject the result in my sorted file Array I get: In your example 1 1 10 10 -> 2 20 -> 22 : It is still (20 + 2) + 22 CC so 42 CC*ĬC: Comparison or copy: this is the ops I count for a complexity of 1. My first naive impression was simply sort the files by sizes and begin with the smaller ones: this way you will privilege the elimination of small files during iterations.My proposition is to compute it "on the fly" and let it be not optimal but at least avoid the worse case.

Precompute the graph of all executions is really too big, in the worst case it can be as big as the data you sort.
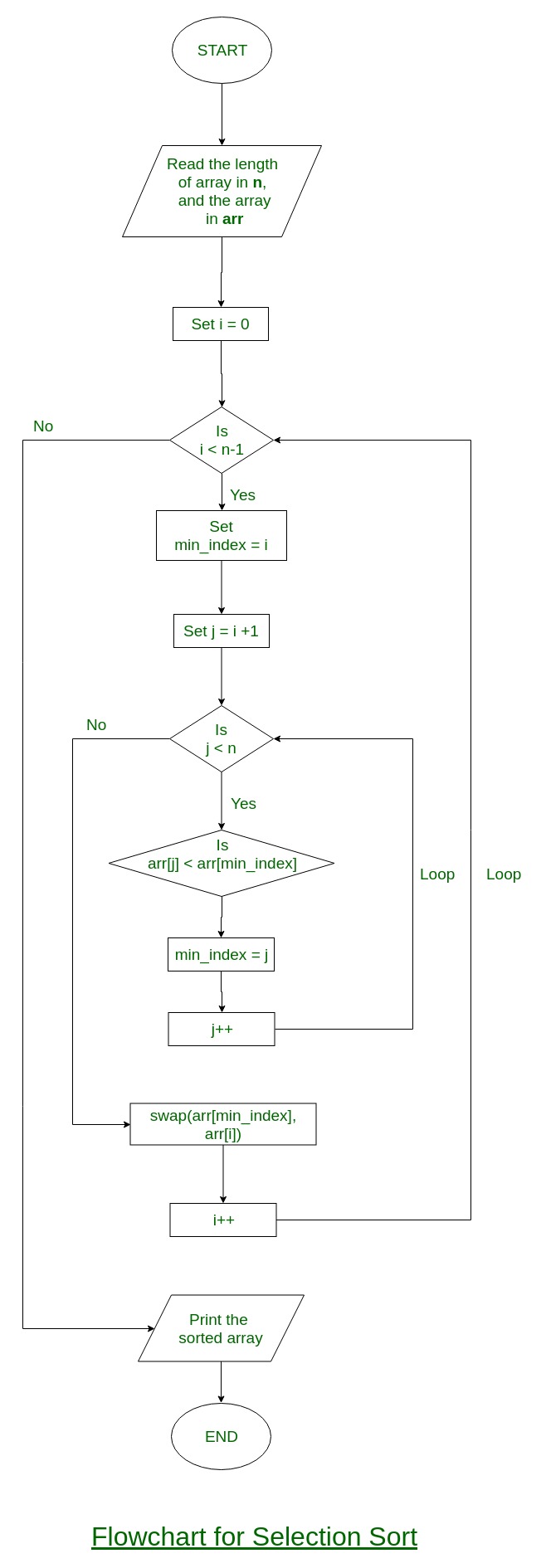
The question is "how to schedule the subsort in an optimal way"? The traditionnal merge sort complexity is o( n.ln(n)) but in my case with different sublist size, in the worst case if one file is big and all the other are small (that's the example you give) the complexity may be o( n.n ) : which is a bad performance complexity. Moreover, I cannot shake the feeling that there might be an "analytical" solution to this problem, or at least a simple heuristic that comes very close to optimality. The problem with this solution is that the amount of nodes explodes, even with a modest number of files (say hundreds) and even after applying some sensible constraints (like sorting the files on size and allowing only merges of the top 2.k of this list). I can then use a shortest path algorithm to determine the optimal sequence. All possible merge states can be ordered into a directed graph (which is a lattice I suppose) with the number of ops to move from one state to another attached to each edge as the cost. My solution for picking the right number of consumers at each step is the following. By contrast, if we use only 2 consumers in the first step and 3 in the second step, the merge pattern ((1,1),10,10) takes only 2+22=24 ops. The merge sequence ((1,1,10),10) leads to 12 read/write operations in (inner) step 1 and 22 operations in (outer) step 2, making a total of 34 ops. Start with 3 consumers in the first step. We need two merge steps to merge all files. Consider the case of 4 files with 1, 1, 10 and 10 records respectively and 3 consumers. The challenge is to pick at each step the right files to merge.īecause the files can differ wildly in size, a simple greedy approach of using all k consumers at each step can be very suboptimal.Īn simple example makes this clear. Because k is (possibly a lot) smaller than n, the merge will be done in a number of iterations/steps. I need to merge n sorted fixed record files of different sizes using k simultaneous consumers, where k

 0 kommentar(er)
0 kommentar(er)
